Institute of Oceanology, Chinese Academy of Sciences
Article Information
- LOU Qi, LI Zhengyan, ZHANG Yanwei, FENG Yilei, ZHANG Xueqing
- Impact of typhoon Lekima (2019) on material transport in Laizhou Bay using Lagrangian coherent structures
- Journal of Oceanology and Limnology, 40(3): 922-933
- http://dx.doi.org/10.1007/s00343-021-0384-7
Article History
- Received Oct. 26, 2020
- accepted in principle Dec. 14, 2020
- accepted for publication Jun. 14, 2021
2 Key Laboratory of Marine Science and Numerical Modeling, Ministry of Natural Resources (MNR), Qingdao 266061, China
The typhoon (also known as tropical cyclones or hurricane) is one of the most serious natural disasters. It can cause direct effects include storm surges, winds, waves, and precipitation, and indirect effects include changes in ocean dynamics that consequently impact the ocean environment (Ezer, 2018). During the typhoon, the concentration of material in the river, wetland, and estuary changed significantly (Yang et al., 2012; Wang et al., 2016; Lin et al., 2019a, b). Freshwater discharge, depressed salinity, and nutrient enrichment could additionally influence the ecosystem in the estuary (Herbeck et al., 2001; Paerl et al., 2001). A typhoon passing over the ocean can cause strong mixing and upwelling, bringing about the low temperature and nutrient-rich water of bottom layer to the upper layer region (Chen et al., 2012; Jiang et al., 2020), and then invoke a mesopelagic ecosystem response (Zhou et al., 2012; Pedrosa‐Pàmies et al., 2019). In addition to the effects of upper ocean, typhoons (hurricanes, tropical cyclones) can cause horizontal material transport, as seen for example of terrestrial material transport to the southern Okinawa during the typhoon Morakot (He et al. 2014), material transport in the coastal northern South China Sea during the typhoon Merbok (Jiang et al., 2020), the Florida current transport and Gulf stream transport during the hurricanes (Ezer, 2018).
The main research methods to study the impact of typhoon on the material transport in the ocean are the sampling and satellite remote sensing (Morimoto et al., 2009; Chen et al., 2012; He et al., 2014). But these two methods are limited by the meteorological condition. Therefore, the numerical model has become a powerful tool for the research of material transport during typhoon passage. In recent years, some research focus on the effects of typhoon on the sea surface temperature, sea surface height, and chlorophyll a in the ocean (Chen and Tang, 2011; Sun et al., 2016; Liu et al., 2019b).
We chose the Lagrangian coherent structure (LCS) method, a method under Lagrangian perspective to study on the material transport, by which transport and mixing in fluid flows driven by dynamical systems theory can be described (Aurell et al., 1997; Ser-Giacomi et al., 2015). The LCS method is in the Lagrangian framework. As the hidden skeleton of fluid flows (Peacock and Haller, 2013), LCSs provide direct geometric information about the motion of inertial particles, which is helpful to understand material transport (Peng and Dabiri, 2009; Rypina et al., 2011). LCS is widely used to study the structures of flow field in the ocean, atmosphere, and even human blood (Peacock and Haller, 2013; Garaboa-Paz et al., 2015; May-Newman et al., 2016; Niang et al., 2020), and also the distribution of matters in water bodies (Lehahn et al., 2007; Olascoaga et al., 2008; Maps et al., 2015; Son et al., 2016), and transport and mixing of water masses (Bettencourt et al., 2012; Duran et al., 2018; Wei et al., 2018). Shadden et al. (2009) showed that LCSs remain valid separatrices when the data are subject to large experimental errors. Therefore, there are many scholars who use LCS method for analyzing transport of materials (Ku and Hwang, 2018; Nolan et al., 2020; Suara et al., 2020). However, the LCS method is rarely used to study the impact of short-term extreme wind on material transport.
Laizhou Bay (LZB), located in the south of Bohai Sea, is a traditional spawning, hatching, and feeding ground for many important economic organisms and has been the focus of scholars' research for a long time (Zhuang and Gao, 2015; Xu et al., 2017; Liu et al., 2019a). Historically, there were a few northward typhoons that affected the Bohai Sea area (Feng et al., 2018). During 1960–2013, there were 88 tropical cyclones that might cause disastrous impacts on Bohai Sea, with an average of 1.63 per year (Wen et al., 2016). The LZB is a semi closed sea area, and the seafloor near the coast is shallow, when a tropical cyclone moves northward, it is easy to cause serious marine meteorological disasters. At present, little attention has been paid to how typhoons affect the material transport in the bay. In this work, LCS were used to describe the transport of floating materials in the Laizhou Bay, Yellow Sea, following the event of typhoon Lekima (2019), to unveil the structures responsible for the tidal and typhoon-induced transports of the upper water, and can be a reference for exploring such an approach for disaster management particularly in the areas of clean-up operation and non-live related asset search after such events.
2 DATA AND METHOD 2.1 Lagrangian coherent structuresAn off-line particle tracking model was used to calculate the trajectories of particles on the basis of the flow field data forced by tide and typhoon. The particle motion equation is as follows:
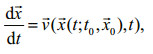 (1)
(1)
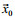
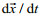

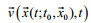
Particles were seeded every 50 m at time t=0. The particle position is updated every hour using the fourth-order Runge-Kutta sub-time stepping scheme. We focused on the horizontal transport of particles.
There are many methods to obtain the LCSs, such as Lagrangian descriptors (Mancho et al., 2013), fuzzy clustering analysis (Froyland and PadbergGehle, 2015), Finite-time Lyapunov exponent analysis (Haller, 2011), spectral clustering algorithm (Hadjighasem et al., 2016), and Lagrangian-Averaged Vorticity Deviation (Haller et al., 2016). Among them, the Finite-time Lyapunov exponents (FTLE) is the most popular because of its simplicity and low computational complexity.
FTLE is a finite time average of the maximum expansion rate for a pair of particles advected in the flow (Shadden et al., 2005) during the period from t to t+T. The FTLE is calculated as:
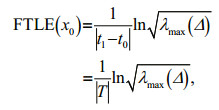 (2)
(2) (3)
(3)where T is integration length, λmax(Δ) is the maximum eigenvalue of a symmetric matrix Δ, and φ is the spatial deformation gradient tensor of the motion trajectory from t to t+T.
Using finite-differencing with values at the neighboring grid points can obtain the spatial gradient of the flow map at each point in the initial grid (Haller, 2001; Lekien et al., 2005; Shadden et al., 2005). The deformation gradient tensor φ in a two-dimensional space is calculated by Eq.4:
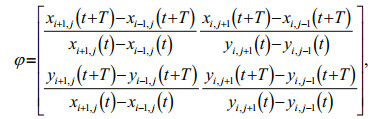 (4)
(4)where x and y are spatial coordinates, and i and j are grid node numbers.
LCS is defined as the ridges of FTLE fields and lines of local maximum with a steep gradient, which can be easily identified in the FTLE fields (Huhn, 2012). Although FTLE ridges are not always perfect indicators of the LCSs (Haller, 2002; Shadden et al., 2005), they perform well in a large number of applications (Peacock and Dabiri, 2010).
Equation 2 can be integrated in either forward or backward time. When the time goes from t0 to t1, the forward time integration identifies ridges of repelling LCS (rLCS). This can be understood as material transport line or surface. When the time goes back from t1 to t0, the backward time identifies attracting LCS (aLCS), which can be understood as the accumulation line or the boundary of the accumulation area during the material transportation (Hsu, 2013). In this study, the LCS represents the rLCS and aLCS, we focus on the path of materials transport, which corresponds to the rLCS.
In this study, time variant double gyre flow field is used to prove the feasibility of the program. The calculations of the FTLE field were programmed by MATLAB. The calculation results of the FTLE fields (Fig. 1) is consistent with those of Jakobsson (2012), which shows that the calculation program can be used for subsequent calculation.
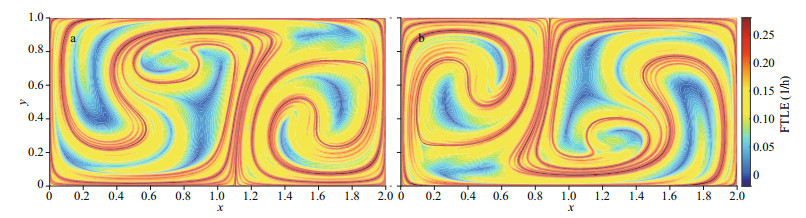
|
| Fig.1 The forward FTLE field (a) and backward FTLE field (b) of the double gyre with the same parameter values of Jakobsson Johan (2012) |
Finite volume community ocean model (FVCOM) is used to simulate the current field of the study area. In the model, coordinate transformation was used to represent the complex bottom slopes and surface elevations. The model area included the entire Bohai Sea (Fig. 2a). The open boundary at the eastern edge of the model area extended cross through the Yellow Sea from Chengshantou to Dandong City. The horizontal resolution can vary spatially, and the grid scale ranged from 200 m in coastal areas to 5 000 m near the open boundary. In three dimensional (3D) simulations, the vertical grid is defined following the sigma coordinates approach, divided into five layers. In this study, the surface velocity is used to calculate the FTLE. The water depth data is based on the Electronic Chart (11 011 and 11 800) published by the The Navigation Guarantee Department of the Chinese Navy Headquarters in 2014, combined with the measured data. The water depth of each grid node in the calculation area is obtained by linear interpolation. The bottom roughness value is treated as a constant of 0.001 0 m. The initial water level and velocity of the entire simulated flow field were set to zero, and the boundary forcing conditions are tide and runoff. The runoff data of the Huanghe (Yellow) River refer to the data of the Huanghe River Network (http://www.yrcc.gov.cn/dt/). The model is forced by four primary tidal constituents (M2, S2, K1, and O1) at the open boundaries. The calculation time of the model is from Jun. 1, 2019 to Aug. 31, 2019. The time step was set to 1 h for all experiments in this study.
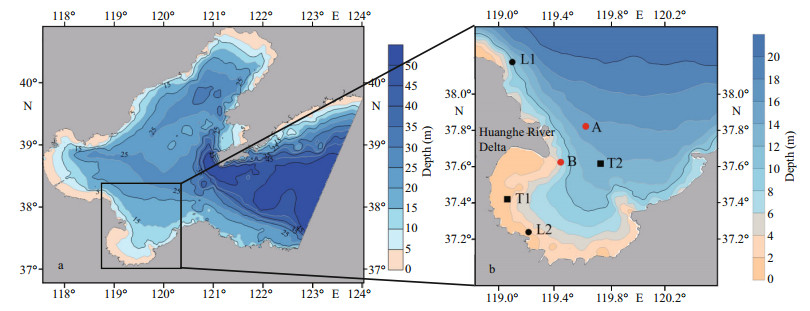
|
| Fig.2 Water depth of hydrodynamic model area (a) and the study area (b) L1 and L2 are water level verification stations; A and B are the current stations; T1 and T2 are representative stations of water level. |
The sea surface wind data is obtained from European Centre for Medium-Range Weather Forecasts (ECMWF), and the Fifth-generation Reanalysis (ERA5) dataset is applied in this study. ERA5 provides the higher time resolution (hourly), and the finer spatial resolution (0.25°×0.25°). The dataset covers the time range from August 9 to 13, 2019.
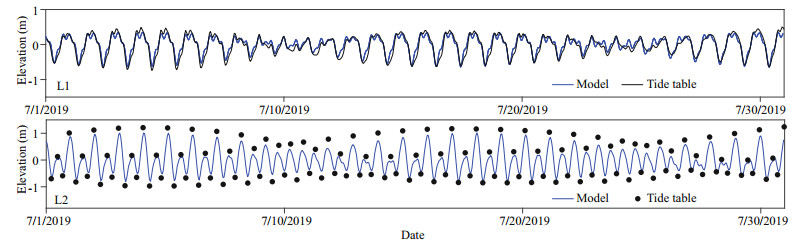
3 RESULT AND DISCUSSION 3.1 Model validationIn order to verify the accuracy of the model, we selected two stations in the LZB from tide tables (NMDIS, 2018), and compared the simulated water lever with the results in the tables (Fig. 3). Pearson correlation coefficient between model results and forecast data is 0.921 at L1, and 0.989 at L2. This shows that the tidal simulation results are credible.
|
| Fig.3 Comparisons of the data from tide tables and computed water levels during July 1–31, 2019 at L1 and L2 |
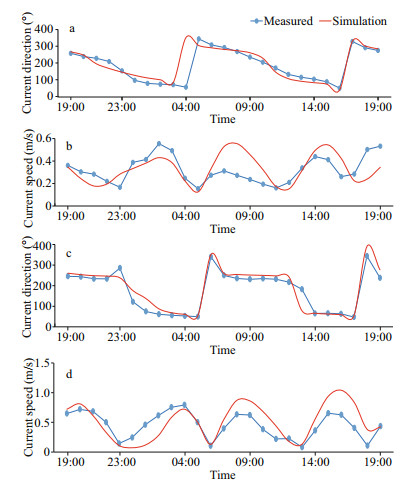
The current velocity at the two stations A (37°37ʹN, 119°23ʹE) and B (37°48ʹN, 119°32ʹE) was monitored at 1-h interval from 19꞉00 on June 6, 2016 to 19꞉00 on June 7, 2016. The time series comparison of surface current speed and direction between model and the observations are shown in Fig. 4 (the measured values are in blue and the numerical simulations are in red). The simulated results of the flow direction and current speed fit well with the observation results at station B. Near the station A, it not fit very well, due to the amphidromic points of Lunar Semidiurnal Tide (M2) and Solar Semidiurnal Tide (S2), where the flow field is complex. The reason also could arise from lower accuracy of the current meter instrument and position errors that are intrinsic to the and GPS-tracked drifters. In general, the model can provide reasonable hydrodynamic driving conditions for particle tracking.
|
| Fig.4 Comparisons of the current direction and speed from the simulation values and measured values at stations A (a and b) and B (c and d) |
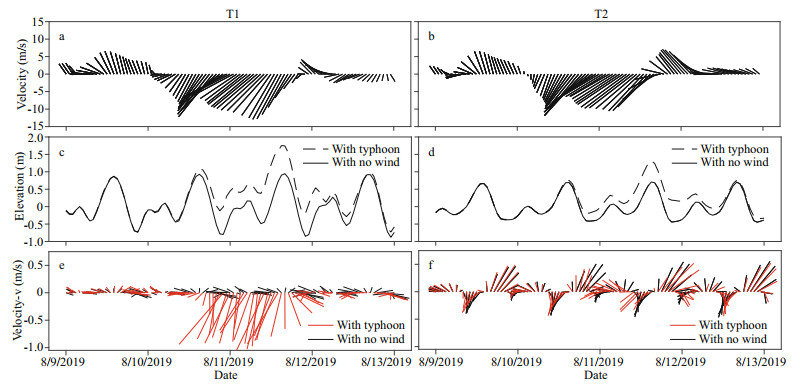
Water level and currents in LZB are numerically simulated by FVCOM. The results are shown in Fig. 5 at representative stations T1 and T2. From August 10–12, 2019. The wind direction on the sea surface changed from southerly to northerly, and the wind speed increased to the maximum of 17 m/s. The water level change is slightly delayed, and the obvious flood time is about half a day later than that in gale period. The speed of surface currents flow into the LZB increases during the high tide up to more than 1.5 m/s. The current directions of the coastal seawater in LZB have changed from longshore to onshore. For T2 station at the mouth of the bay, the westward component of the velocity increases, which make the velocity slightly decrease at ebb tide and increases slightly at flood tide. However, the overall change is not as obvious as that inside the bay. All the velocity changes mean that pollutants in the Huanghe River estuary are easy to enter and accumulate in LZB. At the same time, the pollutants in LZB are difficult to transport out of the bay.
|
| Fig.5 Wind speed and direction (a and b), sea surface tidal elevations (c and d) and currents (e and f) at stations T1 and T2 |
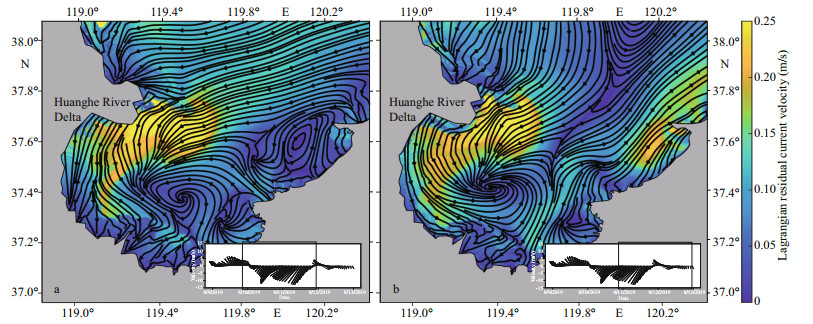
Lagrangian residual current is defined as the displacement of a water particle divided by the corresponding time interval. The Lagrangian residual current filed can be calculated using the numerical methods based on particle tracking. The results are shown in Fig. 6 under tide condition and Fig. 7 under the condition of tide and typhoon.

|
| Fig.6 Lagrangian residual current streamline at flood tide (a) and ebb tide (b) for 50 h The illustration on the lower right corner of each figure is the time series of surface elevation at station indicated as the red dot. The black dot indicates the starting time of residual current. |
|
| Fig.7 Lagrangian residual current streamline for 50 h shown in the box at the lower right corner, with start time of 20꞉00, August 9, 2019 (a) and 21꞉00, August 10 (b) The illustration on the lower right corner of each figure is the time series of wind speed at station in Fig. 5 |
Figure 6 shows that the residual current of the whole LZB is small, the average is 0.01 m/s, and the maximum is ~0.08 m/s. For the different initial moments, the residual current changes greatly. At high tide, water flows into the bay from the east, forming a clockwise vortex in the north of the bay, and an anticlockwise in the middle. However, at the falling and low tide, the water in the Huanghe River estuary flows southward, then anticlockwise circulation northward in LZB, and flows out from the northwest with the current from the East. The results of the two moments are consistent with those of Zou et al. (2018). There is a clockwise residual current vortex at the south of the old Huanghe River estuary in the west of LZB. The direction of residual current in the bay in this study is basically the same as that from observation stations in LZB in Chen et al. (2015). It is also consistent with the conclusion that an anticlockwise circulation is formed in the western part of the bay.
The typhoon has greatly changed the residual current field. Figure 7a covers 50 h of the gale period. The residual currents of the whole LZB flow into the bay, and its direction is basically the same as the wind. Due to the influence of sea surface wind field, the clockwise vortex in the south of the Huanghe River delta disappeared, and an anticlockwise circulation is formed in the middle of the bay. The time period in Fig. 7b covers the later period of the gale and the period when the typhoon passes. The water flows from the west of the bay mouth, and then forms an anticlockwise vortex in the middle of LZB. The water in the east of the bay flows out from northward along the coast. The average value of residual current is about 0.098 m/s, and the maximum is greater than 0.3 m/s.
3.4 Tide induced rLCSsThe Lagrangian residual current depends on the time when a particle starts to move. In contrast, LCS is a more robust description. In this study, the effects of particle release time and integral duration on LCSs were analyzed through scenario experiment.
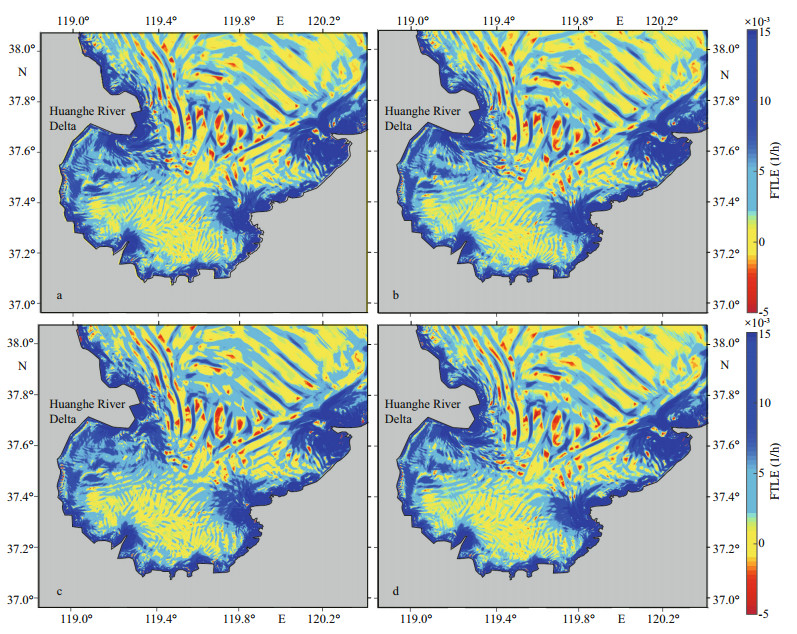
In scenario experiment 1, the effect of integral duration of particle tracking on FTLE field is studied. This study takes forward-time FTLE as an example. In the simulated hydrodynamic field, the particles are uniformly released at a 200-m interval. The FTLE field in LZB is obtained by calculating the FTLE value every 200 m. Figure 8 shows the distribution of FTLE field at different integral duration. The coherent structures were initially formed in 50 h and became stable after 200 h.

|
| Fig.8 Forward FTLE fields for integration time 50 (a), 100 (b), 200 (c), and 300 (d) h at flood tide (5꞉00 on August 9) |
The probability statistics of different results are carried out with integral duration of 50, 100, 200, and 300 h. The statistical results are shown in Fig. 9. Most values of the FTLE in LZB are from -0.005 to 0.01, and the probability distribution of each group is basically the same. Therefore, when calculating the tidal Lagrangian coherent structure in LZB, the integration time can be selected as 50 h to save calculation time. At the same time, the statistical results show that LCS is not sensitive to the change in integral duration.
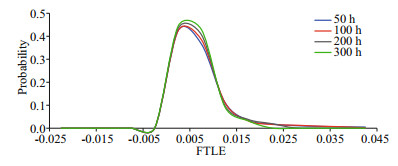
|
| Fig.9 The probability density distribution of FTLE |
Scenario experiment 2, the effect of particle release time on FTLE field is studied. The initial distribution of particles is the same as experiment 1. The results are shown in Fig. 10. There is almost no difference in the direction and position of the FTLE values at the four typical particle release moments (high tide, flooding, low tide, and low tide). Results show that when the integral time is 50 h, FTLE field is not sensitive to the particle release time in LZB, because the tide of LZB is a ~25-h cycle of regular semidiurnal tide.
|
| Fig.10 Forward FTLE fields for integration time 50 h at flood tide (a), high tide (b), ebb tide (c), and low tide (d) The time series in the lower right corner of the figure contains time from 0꞉00 on August 9 to 2꞉00 on August 11. |
Taking the integrated 50-h FTLE field as an example, the LCS structure in LZB is analyzed. Figure 9 shows the distribution of forward-time FTLE fields. The ridge of the FTLE is the rLCS, which can be easily detected from the FTLE field.
The values of FTLE are mainly positive. It shows that there is a high degree of substance separation and a high degree of water mixing on the water surface. The values of FTLE in the middle region of LZB are low (close to zero): these indicate regions with poor exchange of the upper water, and there is a barrier to transport between regions of strong and weak mixing. If pollution is injected in this region of poor mixing, it will remain there for a long time, while pollution injected in a large FTLE region spread rapidly. It indicates that the transportation time of floating pollutants from the bay to the outside is longer. Affected by the topography of the Huanghe River estuary, there are banded rLCSs outside the Huanghe River delta, indicating that the materials from the Huanghe River into the Bohai Sea tend to transport in southeast- northwest direction. Due to the influence of shoal topography in LZB, the obvious rLCSs indicate that the material diffuses strongly in the eastern part of LZB, around Diaolongzui and Longkou headland.
3.5 Tide and typhoon induced rLCSsUnder the combined action of tide and the strong wind during typhoon, the values of forward FTLE in LZB increased. The ridge line moved eastward, and the banded rLCSs disappeared outside the Huanghe River delta in Fig. 11a. This indicates that the diffusion ability of material has been strengthened.

|
| Fig.11 The forward FTLE fields in LZB at mid-range time (a) and the latter half time (b) of typhoon The time series of wind field at the bottom of the picture is the same as that in Fig. 7. |
Most of the forward FTLE values in the southern coastal area of LZB are negative, which indicates that the material in the coastal area is transported to the shore under the operation of a northward wind field. However, there is a banded channel parallel to the coastline from the outer edge of the Huanghe River estuary, which makes it difficult to transport the coastal materials to the sea. There is a patchy area in the middle of LZB, where material tends to accumulate. The dynamic mechanism can be reflected by the residual current field in Fig. 7. There is a strong counterclockwise residual current vortex in this area.
In the latter half time of the typhoon in Fig. 11b, the material transport channel along the coast moves towards the shore, and the trend of material transport to the shore decreases. The patchy area in the middle of the bay still exists, indicating that the material accumulated in this area is not easy to diffuse.
3.6 Comparison of LCSs and satellite remote sensing resultsSince the instantaneous distribution of the floating material approaches to attracting material curves which related to the backward FTLE, we compared structures in the satellite images with the backward FTLE fields.
We collected the Sentinel-2 L1C satellite images before and after the typhoon Lekima in 2019. The different color in satellite images mainly comes from the distribution of suspended particles, which is affected by many processes such as material transportation and bottom resuspension. In this study, we compare the calculated backward FTLE fields with the structures in satellite images. High backward FTLEs show maximum attraction, which act as barriers to transport and mixing. There is no flux across an LCS, and hence LCS can divide a flow into regions with disparate properties (May-Newman et al., 2016).
In the condition of tide, the area with high concentration of suspended solids (region 2 in Fig. 12a) near the Huanghe River estuary before typhoon is consistent with the high value region in backward time FTLE field. The region of the low concentration area (region 1 in Fig. 12a) is basically consistent with the low value area of aLCSs nearby. After the typhoon, the FTLE values increase in the bay. The material accumulation area around the Huanghe River delta still exists (region 3 in Fig. 12b). The banded aLCSs in the middle part of the bay (lines a–c in Fig. 12b) prevented the mixing of material on both sides. The material accumulated in the middle of the bay is not easy to spread to the outside of the bay, which is consistent with the results of forward calculation.

|
| Fig.12 The Sentinel-2 L1C satellite images (a and c) and backward FTLE fields (b and d) before (August 8, 2019) (a and b) and after (August 15, 2019) (c and d) Lekima passing The area with high concentration of suspended solids (region 2 in a and region 3 in c) near the Huanghe River estuary is consistent with the high value region in backward time FTLE field. The banded aLCSs (lines a–c) prevented the mixing of material on both sides. |
It approved that using LCSs to describe the material transport and spatial distribution was reliable.
4 CONCLUSIONBased on FVCOM model, the Lagrangian coherent structure is introduced to study the fluid transport process in the Laizhou Bay under the condition of tides and typhoon. The Lagrangian coherent structure is not sensitive to the initial time and integral time. Our comparison between the numerical results and the satellite images shows that LCSs can well describe the fluid transport under the influence of tides and typhoon.
There are several banded rLCSs outside the Huanghe River estuary under the tidal condition, which led to the material transport around the headland of the Huanghe River estuary, and a typical arc-shaped suspended matter front is formed outside the Huanghe River estuary. However, under the condition of tide and typhoon, the banded rLCSs outside the Huanghe River estuary disappeared, and the suspended solids were transported eastward. The structure of the suspended sediment front is consistent with that of the rLCS during typhoon. A patch area is formed in the middle of Laizhou Bay corresponding to the Lagrangian residual current vortex. In the near shore area, there is a banded rLCSs parallel to the coastline, and the materials tend to transport along the channel to the east and middle of the bay. The banded aLCSs in the middle part of the bay prevented the mixing of material on both sides. The material accumulated in the middle of the bay is not easy to spread outside the bay.
The LCS method is effective for studying material transportation and distribution during the typhoon in the Laizhou Bay. However, under the strong mixed action of typhoon, the mixing of material in water is a three-dimensional phenomenon. This study is the first step, while full dimensional phenomenon will be captured in the future study.
5 DATA AVAILABILITY STATEMENTThe datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
Aurell E, Boffetta G, Crisanti A, Paladin G, Vulpiani A. 1997. Predictability in the large: an extension of the concept of Lyapunov exponent. Journal of Physics A: Mathematical and General, 30(1): 1.
DOI:10.1088/0305-4470/30/1/003 |
Bettencourt J H, López C, Hernández-García E. 2012. Oceanic three-dimensional Lagrangian coherent structures: a study of a mesoscale eddy in the Benguela upwelling region. Ocean Modelling, 51: 73-83.
DOI:10.1016/j.ocemod.2012.04.004 |
Chen B, Liu J, Gao F. 2015. Suspended sediment transport mechanism in Laizhou Bay. Advances in Water Science, 26(6): 857-866.
(in Chinese with English abstract) DOI:10.14042/j.cnki.32.1309.2015.06.012 |
Chen X Y, Pan D L, He X Q, Bai Y, Wang D F. 2012. Upper ocean responses to category 5 typhoon Megi in the western north Pacific. Acta Oceanologica Sinica, 31(1): 51-58.
DOI:10.1007/s13131-012-0175-2 |
Chen Y Q, Tang D L. 2011. Remote sensing analysis of impact of typhoon on environment in the sea area south of Hainan Island. Procedia Environmental Sciences, 10: 1621-1629.
DOI:10.1016/j.proenv.2011.09.256 |
Duran R, Beron-Vera F J, Olascoaga M J. 2018. Extracting quasi-steady Lagrangian transport patterns from the ocean circulation: an application to the Gulf of Mexico. Scientific Reports, 8(1): 5218.
DOI:10.1038/s41598-018-23121-y |
Ezer T. 2018. On the interaction between a hurricane, the Gulf Stream and coastal sea level. Ocean Dynamics, 68(10): 1259-1272.
DOI:10.1007/s10236-018-1193-1 |
Feng J L, Li D L, Li Y, Liu Q L, Wang A M. 2018. Storm surge variation along the coast of the Bohai Sea. Scientific Reports, 8(1): 11309.
DOI:10.1038/s41598-018-29712-z |
Froyland G, Padberg-Gehle K. 2015. A rough-and-ready cluster-based approach for extracting finite-time coherent sets from sparse and incomplete trajectory data. Chaos: An Interdisciplinary Journal of Nonlinear Science, 25(8): 087406.
DOI:10.1063/1.4926372 |
Garaboa-Paz D, Eiras-Barca J, Huhn F, Pérez-Muñuzuri V. 2015. Lagrangian coherent structures along atmospheric rivers. Chaos: An Interdisciplinary Journal of Nonlinear Science, 25(6): 063105.
DOI:10.1063/1.4919768 |
Hadjighasem A, Karrasch D, Teramoto H, Haller G. 2016. Spectral-clustering approach to Lagrangian vortex detection. Physical Review E, 93(6): 063107.
DOI:10.1103/PhysRevE.93.063107 |
Haller G, Hadjighasem A, Farazmand M, Huhn F. 2016. Defining coherent vortices objectively from the vorticity. Journal of Fluid Mechanics, 795: 136-173.
DOI:10.1017/jfm.2016.151 |
Haller G. 2001. Lagrangian structures and the rate of strain in a partition of two-dimensional turbulence. Physics of Fluids, 13(11): 3365-3385.
DOI:10.1063/1.1403336 |
Haller G. 2002. Lagrangian coherent structures from approximate velocity data. Physics of Fluids, 14(6): 1851-1861.
DOI:10.1063/1.1477449 |
Haller G. 2011. A variational theory of hyperbolic Lagrangian Coherent Structures. Physica D: Nonlinear Phenomena, 240(7): 574-598.
DOI:10.1016/j.physd.2010.11.010 |
He X Q, Bai Y, Chen C T A, Hsin Y C, Wu C R, Zhai W D, Liu Z L, Gong F. 2014. Satellite views of the episodic terrestrial material transport to the southern Okinawa Trough driven by typhoon. Journal of Geophysical Research: Oceans, 119(7): 4490-4504.
DOI:10.1002/2014JC009872 |
Herbeck L S, Unger D, Krumme U, Liu S M, Jennerjahn T C. 2011. Typhoon-induced precipitation impact on nutrient and suspended matter dynamics of a tropical estuary affected by human activities in Hainan, China. Estuarine, Coastal and Shelf Science, 93(4): 375-388.
DOI:10.1016/j.ecss.2011.05.004 |
Hsu K K W. 2013. Hydrodynamic Exchange in Estuarine Perimeter Habitats. University of California, Berkeley.
|
Huhn F. 2012. Lagrangian Coherent Structures: Application to Unsteady Oceanic and Laboratory Flows. Universidad de Santiago de Compostela, Santiago de Compostela.
|
Jakobsson J. 2012. Investigation of Lagrangian Coherent Structures-To Understand and Identify Turbulence. Chalmers University of Technology, Gothenburg, Sweden.
|
Jiang C, Cao R X, Lao Q B, Chen F J, Zhang S W, Bian P W. 2020. Typhoon Merbok induced upwelling impact on material transport in the coastal northern South China Sea. PLoS One, 15(2): e0228220.
DOI:10.1371/journal.pone.0228220 |
Ku H, Hwang J H. 2018. The Lagrangian coherent structure and the sediment particle behavior in the lock exchange stratified flows. Journal of Coastal Research, 85(S1): 976-980.
DOI:10.2112/SI85-196.1 |
Lehahn Y, d'Ovidio F, Lévy M, Heifetz E. 2007. Stirring of the northeast Atlantic spring bloom: a Lagrangian analysis based on multisatellite data. Journal of Geophysical Research: Oceans, 112(C8): C08005.
DOI:10.1029/2006JC003927 |
Lekien F, Coulliette C, Mariano A J, Ryan E H, Shay L K, Haller G, Marsden J. 2005. Pollution release tied to invariant manifolds: a case study for the coast of Florida. Physica D: Nonlinear Phenomena, 210(1-2): 1-20.
DOI:10.1016/j.physd.2005.06.023 |
Lin Y P, Li Y H, Zheng B X, Yin X J, Wang L, He J, Shu F F, Qiao L. 2019a. Evolution of sedimentary organic matter in a small river estuary after the typhoon process: a case study of Quanzhou Bay. Science of the Total Environment, 686: 290-300.
DOI:10.1016/j.scitotenv.2019.05.452 |
Lin Y P, Li Y H, Zheng B X, Yin X J, Wang L, He J, Shu F F. 2019b. Impact of typhoon Matmo (2014) on the distribution of heavy metals in Quanzhou Bay. Anthropocene Coasts, 2(1): 209-228.
DOI:10.1139/anc-2018-0006 |
Liu H Q, Liu G J, Yuan Z J, Ge M, Wang S S, Liu Y, Da C N. 2019a. Occurrence, potential health risk of heavy metals in aquatic organisms from Laizhou Bay, China. Marine Pollution Bulletin, 140: 388-394.
DOI:10.1016/j.marpolbul.2019.01.067 |
Liu Y P, Tang D L, Evgeny M. 2019b. Chlorophyll concentration response to the typhoon wind-pump induced upper ocean processes considering air-sea heat exchange. Remote Sensing, 11(15): 1825.
DOI:10.3390/rs11151825 |
Mancho A M, Wiggins S, Curbelo J, Mendoza C. 2013. Lagrangian descriptors: a method for revealing phase space structures of general time dependent dynamical systems. Communications in Nonlinear Science and Numerical Simulation, 18(12): 3530-3557.
DOI:10.1016/j.cnsns.2013.05.002 |
Maps F, Plourde S, McQuinn I H, St-Onge-drouin S, Lavoie D, Chassé J, Lesage V. 2015. Linking acoustics and finite‐time Lyapunov exponents reveals areas and mechanisms of krill aggregation within the Gulf of St. Lawrence, eastern Canada. Limnology and Oceanography, 60(6): 1965-1975.
DOI:10.1002/lno.10145 |
May-Newman K, Vu V, Herold B. 2016. Modeling the link between left ventricular flow and thromboembolic risk using Lagrangian coherent structures. Fluids, 1(4): 38.
DOI:10.3390/fluids1040038 |
Morimoto A, Kojima S, Jan S, Takahashi D. 2009. Movement of the Kuroshio axis to the northeast shelf of Taiwan during typhoon events. Estuarine, Coastal and Shelf Science, 82(3): 547-552.
DOI:10.1016/j.ecss.2009.02.022 |
National Marine Data and Information Service (NMDIS). 2008. 2019 Tide tables. Vol. 1. from the Yalu River mouth to the Changjiang River mouth. China Ocean Press, Beijing.
|
Niang C, Mancho A M, García-Garrido V J, Mohino E, Rodriguez-Fonseca B, Curbelo J. 2020. Transport pathways across the West African Monsoon as revealed by Lagrangian coherent Structures. Scientific Reports, 10: 12543.
DOI:10.1038/s41598-020-69159-9 |
Nolan P J, Foroutan H, Ross S D. 2020. Pollution transport patterns obtained through generalized Lagrangian coherent structures. Atmosphere, 11(2): 168.
DOI:10.3390/atmos11020168 |
Olascoaga M J, Beron‐Vera F J, Brand L E, Koçak H. 2008. Tracing the early development of harmful algal blooms on the West Florida Shelf with the aid of Lagrangian coherent structures. Journal of Geophysical Research: Oceans, 113(C12): C12014.
DOI:10.1029/2007JC004533 |
Paerl H W, Bales J D, Ausley L W, Buzzelli C P, Crowder L B, Eby L A, Fear J M, Go M, Peierls B L, Richardson T L, Ramus J S. 2001. Ecosystem impacts of three sequential hurricanes (Dennis, Floyd, and Irene) on the United States' largest lagoonal estuary, Pamlico Sound, NC. Proceedings of the National Academy of Sciences of the United States of America, 98(10): 5655-5660.
DOI:10.1073/pnas.101097398 |
Peacock T, Dabiri J. 2010. Introduction to focus issue: Lagrangian coherent structures. Chaos: An Interdisciplinary Journal of Nonlinear Science, 20(1): 017501.
DOI:10.1063/1.3278173 |
Peacock T, Haller G. 2013. Lagrangian coherent structures: the hidden skeleton of fluid flows. Physics Today, 66(2): 41.
DOI:10.1063/PT.3.1886 |
Pedrosa‐Pàmies R, Conte M H, Weber J C, Johnson R. 2019. Hurricanes enhance labile carbon export to the deep ocean. Geophysical Research Letters, 46(17-18): 10484-10494.
DOI:10.1029/2019GL083719 |
Peng J, Dabiri J O. 2009. Transport of inertial particles by Lagrangian coherent structures: application to predator-prey interaction in jellyfish feeding. Journal of Fluid Mechanics, 623: 75-84.
DOI:10.1017/S0022112008005089 |
Rypina I I, Scott S E, Pratt L J, Brown M G. 2011. Investigating the connection between complexity of isolated trajectories and Lagrangian coherent structures. Nonlinear Processes in Geophysics, 18(6): 977-987.
DOI:10.5194/npg-18-977-2011 |
Ser-Giacomi E, Rossi V, López C, Hernández-García E. 2015. Flow networks: a characterization of geophysical fluid transport. Chaos: An Interdisciplinary Journal of Nonlinear Science, 25(3): 036404.
DOI:10.1063/1.4908231 |
Shadden S C, Lekien F, Marsden J E. 2005. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D: Nonlinear Phenomena, 212(3-4): 271-304.
DOI:10.1016/j.physd.2005.10.007 |
Shadden S C, Lekien F, Paduan J D, Chavez F P, Marsden J E. 2009. The correlation between surface drifters and coherent structures based on high-frequency radar data in Monterey Bay. Deep Sea Research Part II: Topical Studies in Oceanography, 56(3-5): 161-172.
DOI:10.1016/j.dsr2.2008.08.008 |
Son Y B, Kim Y H, Choi B J, Park Y G. 2016. Lagrangian coherent structures and the dispersion of green algal bloom in the Yellow and East China Sea. Journal of Coastal Research, 75(S1): 1237-1241.
DOI:10.2112/SI75-248.1 |
Suara K, Khanarmuei M, Ghosh A, Yu Y Y, Zhang H, Soomere T, Brown R J. 2020. Material and debris transport patterns in Moreton Bay, Australia: the influence of Lagrangian coherent structures. Science of the Total Environment, 721: 137715.
DOI:10.1016/j.scitotenv.2020.137715 |
Sun Y J, Pan J Y, Perrie W. 2016. Upper ocean physical and biological response to typhoon Cimaron (2006) in the South China Sea. Lupo, Anthony R. (2016). Recent Development in Tropical Cyclone Dynamics, Prediction, and Detection, 10.5772/61455(Chapter 4). p. 67-87, https://doi.org/10.5772/64099.
|
Wang X M, Wang W Q, Tong C. 2016. A review on impact of typhoons and hurricanes on coastal wetland ecosystems. Acta Ecologica Sinica, 36(1): 23-29.
DOI:10.1016/j.chnaes.2015.12.006 |
Wei X, Zhan H G, Cai S Q, Zhan W K, Ni P T. 2018. Detecting the transport barriers in the Pearl River estuary, Southern China with the aid of Lagrangian coherent structures. Estuarine, Coastal and Shelf Science, 205: 10-20.
DOI:10.1016/j.ecss.2018.03.010 |
Wen L J, Liu G Y, Liu Q R, Ruan C Q, Wang B. 2016. Statistical analysis of tropical cyclones which affected the Bohai Sea during 1960-2013. Ocean Development and Management, 33(8): 84-89.
(in Chinese with English abstract) DOI:10.3969/j.issn.1005-9857.2016.08.018 |
Xu L, Wang T Y, Wang J H, Lu A X. 2017. Occurrence, speciation and transportation of heavy metals in 9 coastal rivers from watershed of Laizhou Bay, China. Chemosphere, 173: 61-68.
DOI:10.1016/j.chemosphere.2017.01.046 |
Yang C P, Yu Y T, Kao C M. 2012. Impact of climate change on Kaoping river water quality. Applied Mechanics and Materials, 212-213: 137-140.
DOI:10.4028/www.scientific.net/AMM.212-213.137 |
Zhou W H, Yin K D, Harrison P J, Lee J H W. 2012. The influence of late summer typhoons and high river discharge on water quality in Hong Kong waters. Estuarine, Coastal and Shelf Science, 111: 35-47.
DOI:10.1016/j.ecss.2012.06.004 |
Zhuang W, Gao X L. 2015. Distribution, enrichment and sources of thallium in the surface sediments of the southwestern coastal Laizhou Bay, Bohai Sea. Marine Pollution Bulletin, 96(1-2): 502-507.
DOI:10.1016/j.marpolbul.2015.04.023 |
Zou T, Zhang L B, Zhang H, Li D. 2018. Hydrodynamic characteristics in the artificial reefing construction area in laizhou bay: based on: a continuous long-term observation. Oceanologia Et Limnologia Sinica, 49(02): 280-289.
(in Chinese with English abstract) |
 2022, Vol. 40
2022, Vol. 40


